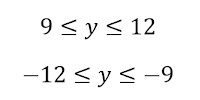Sukkot: Decreasing consecutive integers on the sixth day

 It's common in traditional Algebra I classes to ask students to sum consecutive integers. In 2015, I wrote about how I've used this with younger students on Chanukah.

I've always wanted to use a Sukkot application of this problem, since the Parot He'Chag (bulls of the mussaf offering) are offered as decreasing consecutive integers.

Last year, I did so as a bonus question on my word problems test (in November; this unit's never coincided with Sukkot itself.)

You'll notice that I gave them the sum of the consecutive integers and asked them to find a particular day's number.

First, the students defined their variables and wrote an equation:

Then, they combine like terms and solve for the variable. Note that they solve for the number of bulls offered on the first day.

The final answer, which must be written as a sentence, requires the students to take x=13 and subtract 5 to find the number of bulls offered on the sixth day. 

Only a small number of students attempted this bonus question, but they did a great job. 

Happy sixth day of Sukkot, everyone!

Parshat Matot: What's half of 675,000?

In this week's parsha, the Jews have to divide spoils after defeating Midian, which offers great opportunities for math!

In this D'var Torah that I wrote for the Center for Modern Torah Leadership, I cover an Ohr HaChayim that differentiates between part-to-part and part-to-whole ratios and a Malbim that references equivalent fractions. We also sneak in some thoughts about division, counting and parts of different wholes.

My favorite line is Rav Eliyahu Munk's translation of Ohr HaChayim:

"The Ohr Hachaim accepts Ramban’s question, writing, “למה האריך כל כך בפרטי החשבון בדבר שיכול כל הבא למנות לידע ”, hilariously translated by Rav Eliyahu Munk as “Who amongst us cannot figure out what half of a total of 675,000 sheep amounts to?”"

Who, indeed?

It's not usually taught in Jewish day schools, but there's a lot of math in Matot!

Enjoy. Shabbat shalom!

Rational numbers are like midrashim

I enjoyed reading Ilana Kurshan's memoir "If All the Seas Were Ink."

I especially appreciated how she compares midrash to rational numbers. Join the discussion here.

Lessons Learned: Graphing an Israeli flag on a coordinate plane

Last year, I debuted this "graph an Israeli flag on the coordinate plane" activity in my 6th grade classes. This activity was very successful! I would estimate it takes about 30 minutes to make one graph (I had 15, so two different groups of students made each graph.) Not every group finished, but I just needed a few good finished copies. The kids enjoyed the activity regardless, though some of them got frustrated when they started with markers, made errors and then could not fix them.

Supplies are essential! I did not have enough yardsticks (you need one per group) and blue markers. You need 1 thin blue marker per group and 1 thick blue marker per person. Crayola does not appear to sell boxes of thin markers that are all blue. You don't actually need to do much with the thin markers. They are primarily useful to number the axes.

It is important for visibility that the Magen David is made with a thick marker. You can outline with a thin marker, but you'll need to trace over with a thick one for it to be seen, as you can tell in the difference between these two graphs.

One last change: I used axes that were not blue, and I thought it looked good. The goal of contrast was that the axes not impede the visual of the Magen David.

This was fun. I'm hoping to do it again this year!

What's new?

This week's parsha is Parshat Noach. Check out my lesson from last year here.

I also recently wrote up some reflections for JOFA about my experience layning Torah for the first time. You can find it here.

Beta: Graphing an Israeli flag on the coordinate plane for Yom Ha'atzmaut

It's rough having math class on Yom Ha'atzmaut. It's supposed to be math class, but YH"A is supposed to be the most awesome day of the year. How do we make them both happen?

I've done a number of activities over the years for YH"A, some of which I will share in the future. This year's activity is quite beta. There are challenges inherent in doing it properly, which I'll explain later. I generated this set of instructions that utilize the skills my 6th graders have already mastered.

The skills are:
a) Plot points on a coordinate plane.
b) Identify points that are reflections over the x-axis and the y-axis.
c) *Challenge only: Calculate the area of the triangles that form the Magen David on the flag.

If you just want the worksheet, it is here in PDF and Word. 
Screenshots appear at the bottom of the post.

When they are done, their picture should look like an Israeli flag.

(Image from the Wikimedia Commons.)

I started by buying some of these big coordinate grid pads. The kind that are sticky on the back are much more expensive. These are cheaper, although I recognize coordinate grid paper might be outside of some school's budgets. (You can use this activity on a normal piece of graph paper, too.)

I started my making giant axes for the students. For my weakest students I'll label the axis with its numbers, but for the other students, I just made the x-axis and y-axis.

I went through several drafts of the coordinates. The triangles must be equilateral, which means that we use a 30-60-90 triangle to find the side lengths. (Each main triangle on the Magen David is made up of two triangles like the one that appears below.)

(Image from the Wikimedia Commons.)

In a 30-60-90 triangle, if the height is rational, the side length is irrational and vice versa. This means that we have to round if we want the height ( a*root 3) and the side length (2a) to be integers. I approximated by making the side length 14. That makes a=7, which works out to a height of ~12.12.

I stumbled upon this excellent choice - excellent because the height of 12 is divisible by 3, and each triangle is 3/4 of the height of the total Magen David. (As always, I owe this particular insight to my estimable colleague John Watkins-Chow.)

The way I generated my triangle was to choose a top point, use a protractor to center a 60 degree angle around that point, and then create a side length that was close to a lattice point.

Then I moved up or down to center appropriately. I redid it if I thought the star was too large for the page or if it was not centered. I eventually arrived at the points I chose here.

If I was doing this with 8th graders, I would change #3-6 to graphing linear inequalities.

I'll discover on Tuesday how this works, but I encourage anyone who is interested to send me a shot of their graphs that they create.

Chag Ha'atzmaut Sameach!

Edits: The first version of this post neglected to mention John Watkins-Chow's assistance.  

Last night, we counted 10,100 - or was it 202?

Dedicated l'ilui nishmat Dov Nachman ben Aharon Yonah, my paternal grandfather, whose 86th birthday is today. May his memory be a blessing.

Isn't this how you count to 20?

 

We all count Sefirat Ha'Omer in two base systems - base ten and base seven. For example, on day 20, we count "הַיּוֹם עֶשְׂרִים יוֹם שֶׁהֵם שְׁנֵי שָׁבוּעוֹת וְשִׁשָּׁה יָמִים לָעֹֽמֶר", which basically tells us that 20 in base ten is 26 in base seven - two weeks and six days. (In fact, last night we counted 3 (or 11 in binary.) I chose the title of this post because of the time a few years ago when I saw a 6th grader of mine had been practicing her binary Sefirat Ha'Omer in her locker. This was a serious kvell moment for me.*

My interest in base system math was sparked by two things. The first was a class I took at Harvard called "Math For Teaching Arithmetic" (with my amazing professor Bret Benesh) where we invented and used our own number system to model how kids learn arithmetic. If you think long division is tough, you should try it in binary. That's rough! But most math teachers don't find long division tough, so these activities really helped us get into the heads of struggling students. The second impetus to begin the Binary Sefira project was a math team my strongest students were on. Though I was not coaching the math team, they were assigned base system problems during their competitions and they didn't know what base systems were.

For example, 10,100 in binary is 202 in what base? (Hence the title.) This is a challenging problem because most of us think in base 10 and would naturally turn 10,100 into 20 first before trying to figure out in which base 20 would be written as 202.* This is definitely a higher-level problem, so first, let's examine how this material would be taught to middle school students who would benefit from enrichment.

Base system work is an ideal extension - it's intellectually demanding, reinforces understanding of place value and exponents, and, most importantly, it is an entirely separate topic not in most curricula. Essentially, you're enriching the students without teaching the material someone else is planning to teach them next year. It fits the criteria for high-quality challenge materials. It's not for every kid, though most of our students are very comfortable answering the question "What time will it be in 12 hours?" Telling time, also known as "clock math" is math in a different base system.)


How to introduce the topic
With my initial groups of students, they knew what different base systems were from their math team, so we just jumped right in. For the first 3-5 days after Pesach, I would write the Sefira on the board in various different base systems, increasing the number of base systems every day. At first, I put the 'binary Sefira' (my term for Sefira in multiple base systems) up on the board. After a few days, student volunteers would put binary Sefira up on the board. There was a gradual build to comfort and mastery - over a period of 49 days, you can say to students, "You'll be more comfortable next week."

Teaching Explicitly

After a few years, I started getting students who had not worked with other bases on the math team. I also always had a few weaker students in my class for whom it was not as obvious. I began to introduce the concept with explicit instruction. 

So how does it work?

The column you think of as the "ones" column could also be described as the 10^0 column. It tells you how many 10^0 (ones) you have. When  that column fills up, we need to regroup into the 10^1 column. If the tens column fills up (i.e., you have ten groups of 10), you need a 10^2 (or hundreds) column.

As I mentioned before, we count Sefira in two bases - base 10 and base 7. Base 7 is a big enough base that we only get to the 7^1 column filling up on the last day. There is a beautiful mathematical and religious synergy to the fact that we count 7 weeks of 7 days - perhaps worthy of a Shmita or Yovel post another day.

When turning base 10 numbers into much smaller bases, we have to regroup really quickly. For all the big bases, day 44 is still in double digits. But for binary and base 3 (below), it's another matter.

Binary:

The procedure I teach kids is to think of the biggest power of two that can be subtracted from the target number (in this case, 44). The answer, 32, is in the 2^5 column. That tells us we're going to have to fill 6 columns. In my early years, I liked to write the exponential expression that was the size of the column below the blank line. It clarified which column was which but made them look too confusingly like fractions. 

The number above is 44 in base 10: There is a group of 32, no groups of 16, one group of 8 and one group of 4, then placeholder zeroes in the twos and ones column. 

The base 3 number is also quite rich. They have to figure out that the greatest power of 3 is 27, subtract that from 44 to get 17, figure out that 17 has only one 9, subtract that to get 8, and so on. 44 is what I call a "full count" kind of day in base 3, because the addition of one more day would fill the next two columns, leading day 45 in binary to be 1200.

Differentiation
This exercise allows for a lot of differentiation. The strongest students can be most involved in the early days, as I mentioned above. You can also have different kids wrote different numbers on the board. Stronger students can do the smallest bases (binary, base 3) and the largest (base 14, base 15, hexadecimal - more about this later.) Students who are comparatively weaker can do the bases in the middle, such as 5, 6 and 7.

I also love that these worksheets are really easy to make!


Large bases
When you get past base 10, you need additional digits. If you are working in base 11, you need a single digit that represents 10 ones. If you are working in base 12, you need a digit for 10 and a digit for 11. With my students, I've gone as far as hexadecimal (base 16).

Here's the full list for 44.

For bases 11 through 14, the numbers work out nicely. However, since 44 is 2 groups of 15 and 14 ones, in base 15 we need to write it as 2E, with the E representing 14. Similarly, 44 is 2 groups of 16 and 12 ones, so we write it 2C, with the C representing 12.

We generally use A for 10, B for 11, C for 12, D for 13, E for 14 and F for fifteen.

Challenge materials:
Once students have been practicing for a while (for example, on day 44), you can ask them to work backwards in a few ways. The first is turning a number in another base back into base 10. Below, note that 44 is written as a number in bases 5 through 14. You can't have the number 44 in any lower base because none of those have enough room in the 'ones column' or the "tens column" for four groups of anything.
The students are instructed to turn 44 in various bases into numbers in base 10. For example, 44 in base 8 means (4)8^1 + (4)8^0 or 32+4 or 36 in base 10.

Challenge type #2 would be to ask kids to figure out what 44 in base 13 would be in base 7, much like the problem we did right at the beginning. In this case, two base changes are required.

Error analysis is a third way students can be asked to think differently. In the picture below, base 3 is right and base 4 is wrong. You can ask your students:
a) What day is it?
b) What is the correct base 4?
(Answers in *** below.)

Challenge type #4, the hardest by far, is "guess the base". You give the student the number (let's pick 47 in this case) in base 10 and then you say "47 in base 10 is 43 in what base?" In this case, the answer is base 11, so it is somewhat guessable since the two bases are close. However, make it "... is 133 in what base?"**** and it is a lot harder to guess. It has to be reasoned out. (Using, I'll admit, a series of educated guesses.)

Other methods:
There are other methods to calculate numbers in other bases (often referred to as "mod" or "modulo": 3 mod10 = 11 mod2) that don't involve using exponents explicitly, the way I have done in this post. These methods have their own distinct benefits and drawbacks. My colleagues John Watkins-Chow and Dr. Steven Steinsaltz shared two such methods with me, which I may yet summarize in another post. (After all, there are many more days of the Omer ahead of us.)

In conclusion:
I don't know why more strong students are not taught to convert between bases. It strengthens their understanding of place value, exponents and makes their thinking more flexible. Try it in your classroom and let me know how it works!

* Day 20 is also Yom Ha'Atzmaut, though this year Y"HA is pushed off to the 6th of Iyar - stay tuned for a future post for this important holiday.

** It's base 3. (2)3^2 + (2)3^0 = 202 in base 3 or 20 in base 10.
*** (1)3^3 + (2)3^2 + (0)3^1 + (1)3^0 = 27+18+1=46. However, (2)4^2 + (3)4^1=32+12=44. To do 46 in base 4, you need to add 2 ones, so the correct answer would be 232.
****Base 5: 25+15+3